My research interests are quantum information theory and quantum many-body systems. In particular, I am interested in the topics below:
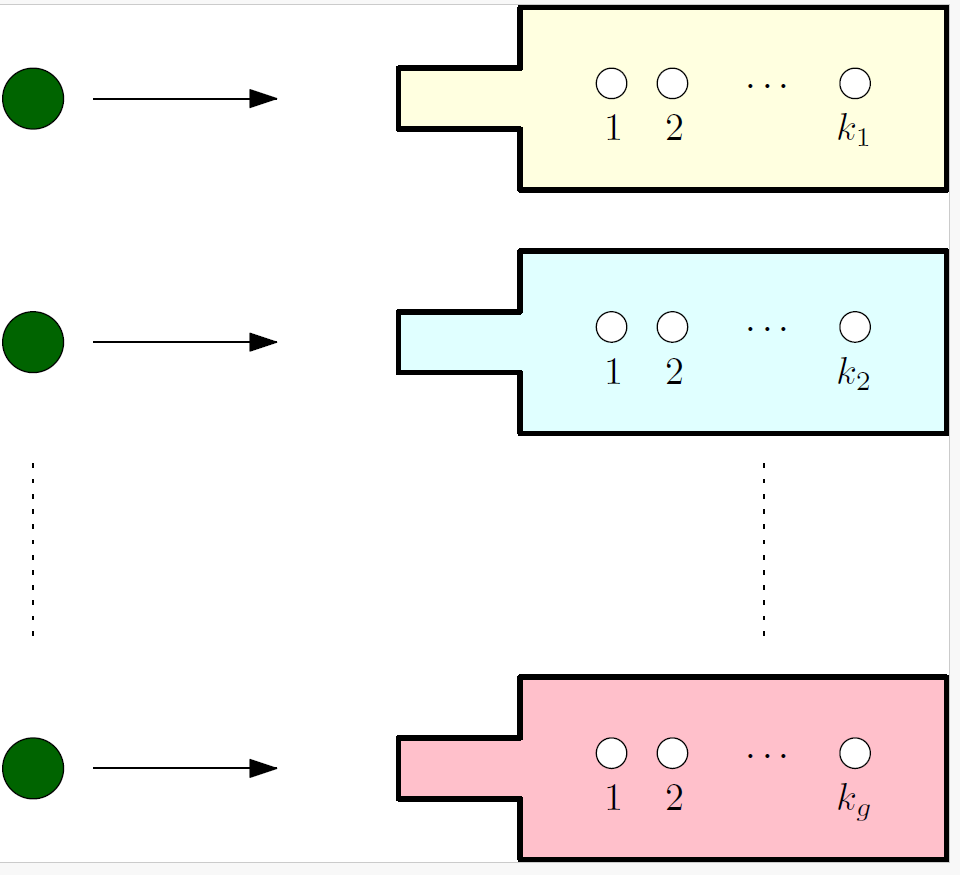
Quantum measurements
Quantum measurements are described by positive-operator valued measures (POVMs). One of the defining features of quantum mechanics is that these measurements can be incompatible, i.e., cannot be implemented at the same time. The best-known example are the position and momentum of a particle. Incompatible measurements are needed for many quantum phenomena, e.g., the violation of a Bell inequality, and therefore also quantum technologies, e.g., device-independent quantum key distribution (DIQKD). As with quantum entanglement, a sufficient amount of noise can destroy measurement incompatibility. That is what makes building a quantum computer so hard. One of the leading question I want to answer in this line of research is how robust measurement incompatibility is to noise.
Find out more about my research on quantum measurements here.
Quantum cryptography
The best known form of quantum cryptography is arguably quantum key distributions, in which two parties want to establish a secret key and quantum mechanics can help them to detect eavesdroppers. However, this is not the only form of quantum cryptography there is. For example, I am working on position-based cryptography, in which the position of a party is used as a credential instead of a secret key. For example, this could be used to verify that a server is indeed located at a bank and not being run by some scammers in a different place. While position-based cryptography is impossible classically, it can be realized with quantum resources. However, many challenges remain that need to be overcome in order to make quantum position-based cryptography a reality.
Find out more about my research on quantum cryptography here.
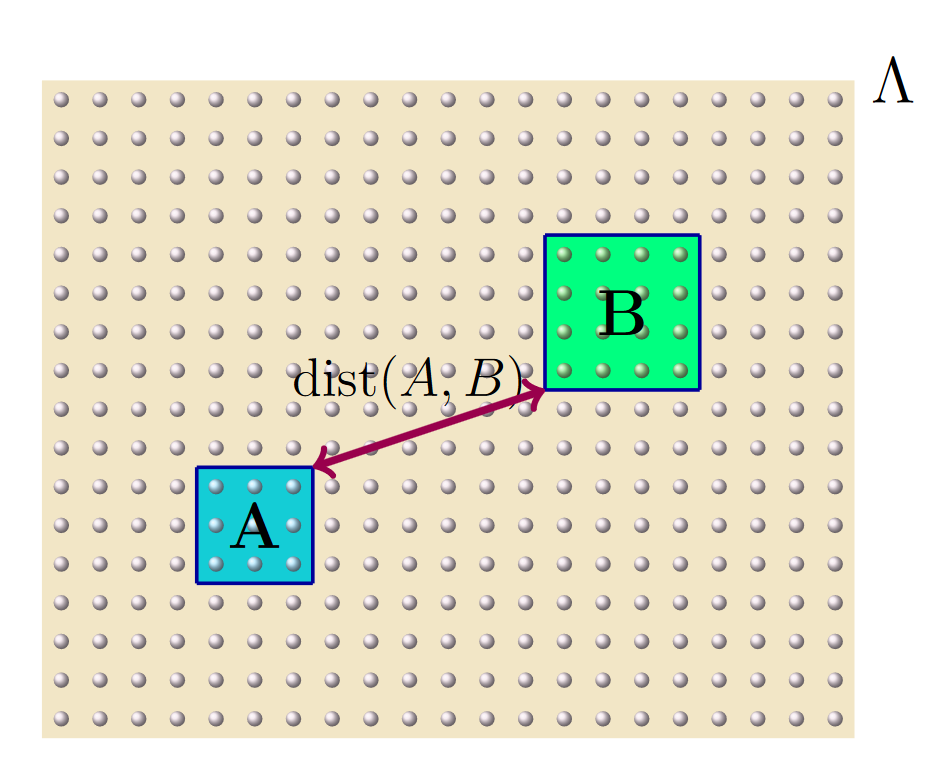
Quantum many-body systems
Quantum many-body systems are systems that do not only consist of one atom, say, but of many. They are interesting from a quantum information theory perspective for two reasons. First, methods from quantum information theory can be used to study them. For example, correlations quantified, e.g., in terms of mutual information determine how difficult it is to simulate a quantum many-body system. On the other hand, we will need some form of quantum many-body system in order to build a quantum computer or quantum simulator. Therefore, we need to know how well we can use these systems to store and erase information, for example.
Find out more about my research on quantum many-body systems here.
Quantum entropies
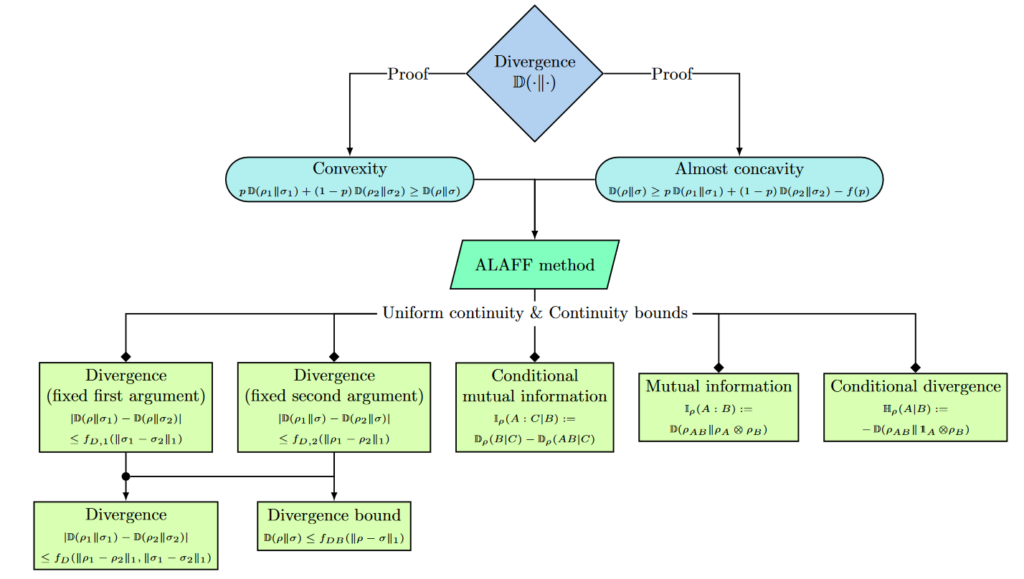
Quantum entropies are a fundamental tool in both quantum and classical information theory. They quantify how well we can perform information processing tasks such as compressing information or testing a hypothesis. We can often evaluate entropies better for some quantum states than for others. Continuity bounds allow us to quantify by how much the entropy of nearby states can differ. Therefore, I have worked, e.g., on finding better continuity bounds for different kinds of entropic quantities.
Find out more about my research on quantum entropies here.
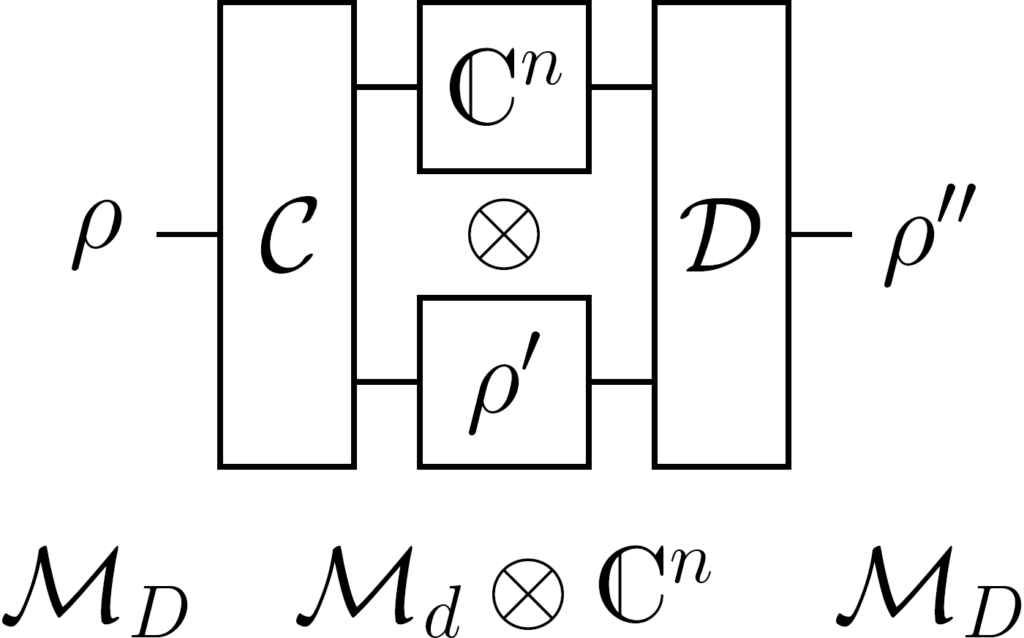
Quantum and classical compression
A fundamental task in information processing is the storage of information. Since quantum memories are very challenging to build and since that difficulty increases with the size of the quantum state to be stored, we have an interest in compressing quantum states as much as possible while preserving their relevant information. Which information is relevant can differ depending on the task at hand. Thus, quantum compression problems arise in different guises, for example in the context of programmable quantum processors. These are machines that should perform different operations depending on the program they are given. We are again intersted in using as little space for these programs as possible.
Find out more about my research on quantum and classical compression here.