Certifying and learning quantum Ising Hamiltonians
with Matthias C. Caro, Francisco Escudero Gutiérrez, Aadil Oufkir, and Cambyse Rouzé
In this work, we study the problems of certifying and learning quantum Ising Hamiltonians, i.e., Hamiltonians with only two-body interactions. First, we provide a nearly-optimal algorithm for certifying an Ising Hamiltonian in normalized Frobenius norm via access to its time-evolution operator. By certifying we mean testing whether the Hamiltonian we are given is close to a fixed Hamiltonian or far from it. To our knowledge, this is the first nearly-optimal algorithm for testing a Hamiltonian property. A key ingredient in our analysis is the Bonami Lemma from Fourier analysis.
Second, we design an algorithm for learning Ising Gibbs states in trace norm that is sample-efficient in all parameters. In contrast, previous approaches learned the underlying Hamiltonian (which implies learning the Gibbs state) but suffered from exponential sample complexity in the inverse temperature.
Finally, we give an algorithm for certifying Ising Gibbs states in trace norm that is both sample and time-efficient, thereby solving a question posed by Anshu (Harvard Data Science Review, 2022). Our last two results extend from Ising Hamiltonians to Hamiltonians with k-body interactions. [arXiv]
Heisenberg-limited Hamiltonian learning continuous variable systems via engineered dissipation
with Tim Möbus, Tuvia Gefen, Yu Tong, Albert H. Werner, and Cambyse Rouzé
Discrete and continuous variables oftentimes require different treatments in many learning tasks. Identifying the Hamiltonian governing the evolution of a quantum system is a fundamental task in quantum learning theory. While previous works mostly focused on quantum spin systems, where quantum states can be seen as superpositions of discrete bit-strings, relatively little is known about Hamiltonian learning for continuous-variable quantum systems. In this work we focus on learning the Hamiltonian of a bosonic quantum system, a common type of continuous-variable quantum system. This learning task involves an infinite-dimensional Hilbert space and unbounded operators, making mathematically rigorous treatments challenging. We introduce an analytic framework to study the effects of strong dissipation in such systems, enabling a rigorous analysis of cat qubit stabilization via engineered dissipation. This framework also supports the development of Heisenberg-limited algorithms for learning general bosonic Hamiltonians with higher-order terms of the creation and annihilation operators. Notably, our scheme requires a total Hamiltonian evolution time that scales only logarithmically with the number of modes and inversely with the precision of the reconstructed coefficients. On a theoretical level, we derive a new quantitative adiabatic approximation estimate for general Lindbladian evolutions with unbounded generators. Finally, we discuss possible experimental implementations. [arXiv]
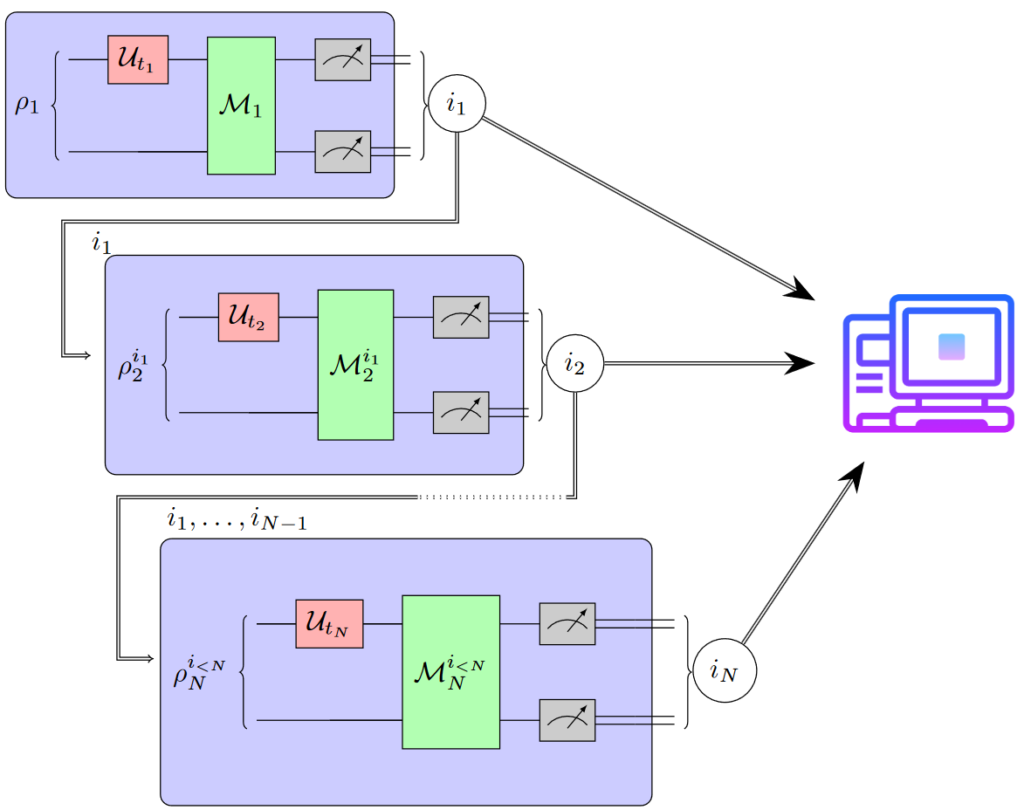
Hamiltonian property testing
with Matthias C. Caro and Aadil Oufkir
Locality is a fundamental feature of many physical time evolutions. Assumptions on locality and related structural properties also underlie recently proposed procedures for learning an unknown Hamiltonian from access to the induced time evolution. However, no protocols to rigorously test whether an unknown Hamiltonian is local were known. We investigate Hamiltonian locality testing as a property testing problem, where the task is to determine whether an unknown n-qubit Hamiltonian H is k-local or ε-far from all k-local Hamiltonians, given access to its time evolution. First, we emphasize the importance of the chosen distance measure: With respect to the operator norm, a worst-case distance measure, both coherent and incoherent quantum locality testers require exponentially many time evolution queries and an exponential expected total evolution time. In contrast, when distances are measured according to the normalized Frobenius norm, corresponding to an average-case distance, we give a sample-, time-, and computationally efficient incoherent Hamiltonian locality testing algorithm based on randomized measurements. In fact, our procedure can be used to simultaneously test a wide class of Hamiltonian properties beyond locality. Finally, we prove that learning a general Hamiltonian remains exponentially hard with this average-case distance, thereby establishing an exponential separation between Hamiltonian testing and learning. [arXiv]
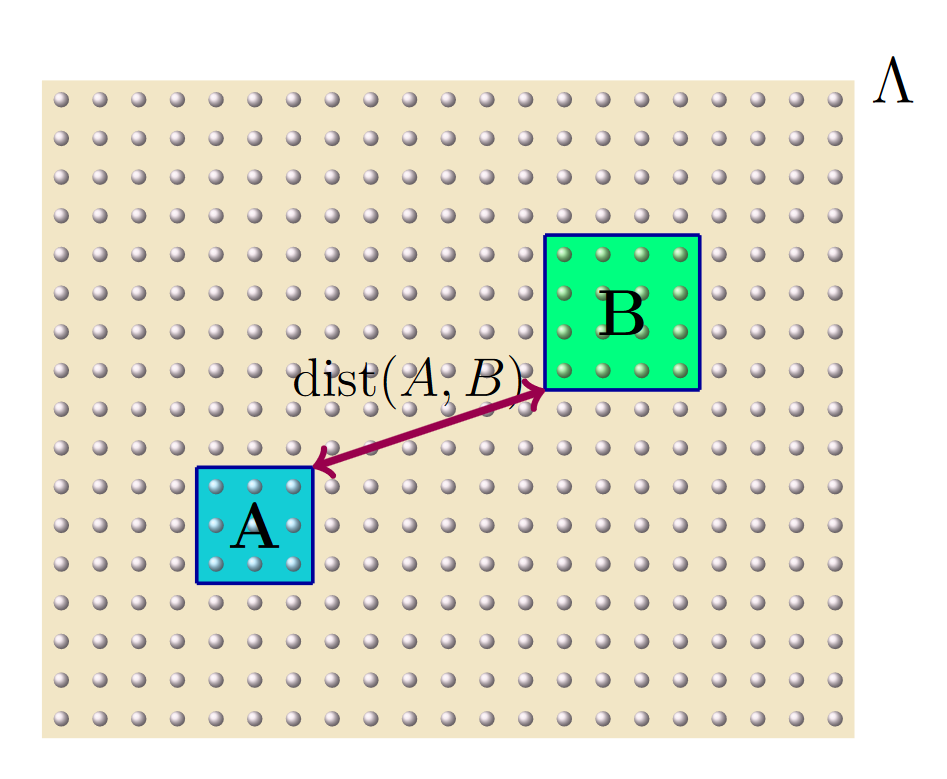
Strong decay of correlations for Gibbs states in any dimension
with Ángela Capel and Antonio Pérez-Hernández
Quantum systems in thermal equilibrium are described using Gibbs states. The correlations in such states determine how difficult it is to describe or simulate them. In this article, we show that systems with short-range interactions that are above a critical temperature satisfy a mixing condition, that is that for any regions A, C the distance of the reduced state ρAC on these regions to the product of its marginals, ∥ρAC(ρA−1⊗ρC−1)−1AC∥, decays exponentially with the distance between regions A and C. This mixing condition is stronger than other commonly studied measures of correlation. In particular, it implies the exponential decay of the mutual information between distant regions. The mixing condition has been used, for example, to prove positive log-Sobolev constants. [journal] [arXiv]
Dissipation-enabled bosonic Hamiltonian learning via new information-propagation bounds
with Tim Möbus, Matthias C. Caro, Albert H. Werner, and Cambyse Rouzé
Reliable quantum technology requires knowledge of the dynamics governing the underlying system, i.e., to learn the system Hamiltonian. In contrast to multi-qubit systems, learning guarantees for bosonic systems have remained mostly unexplored. For m-mode Hamiltonians given as polynomials of bounded degree in annihilation and creation operators with modes arranged on a lattice, we show that a simple procedure based on finite-difference methods works. We then propose an enhanced procedure based on added dissipation that performs even better. Our protocol involves the experimentally reachable resources of (projected) coherent state preparation, dissipative regularization akin to recent quantum error correction schemes, and heterodyne measurements. As a crucial step in our analysis, we establish a new Lieb-Robinson type bound for the evolution generated by an arbitrary bosonic Hamiltonian of bounded degree combined with photon-driven dissipation. [arXiv]
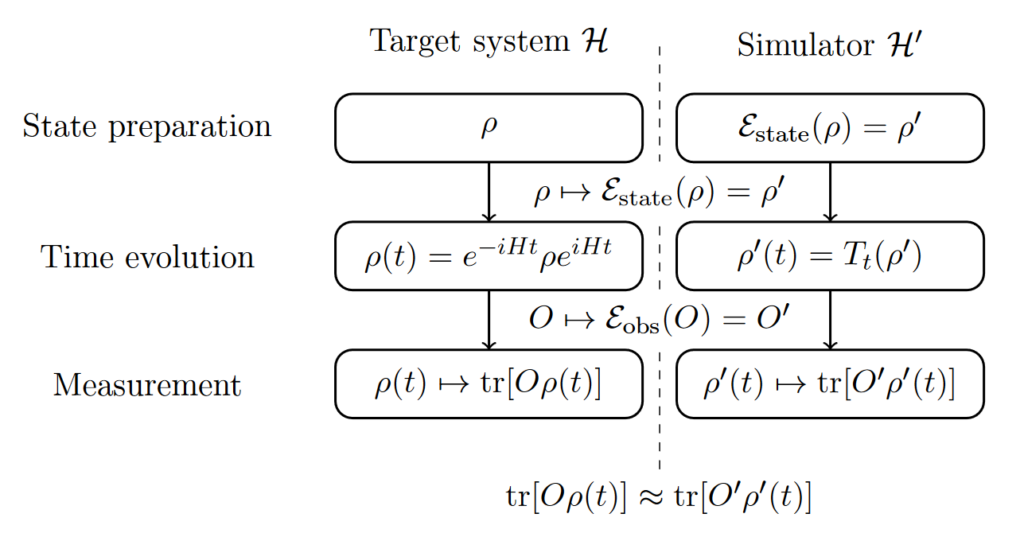
Going Beyond Gadgets: The Importance of Scalability for Analogue Quantum Simulators
with Dylan Harley, Ishaun Datta, Frederik Ravn Klausen, Daniel Stilck França, Albert Werner, and Matthias Christandl
We propose a theoretical framework for analogue quantum simulation to capture the full scope of experimentally realisable simulators, motivated by a set of fundamental criteria first introduced by Cirac and Zoller. Our framework encompasses a range of possibilities for experiment, such as the simulation of open quantum systems and overhead reduction using Lieb-Robinson bounds. We discuss the requirement of scalability in analogue quantum simulation, and in particular argue that simulation should not involve interaction strengths that grow with the size of the system. We develop a general framework for gadgets used in Hamiltonian complexity theory and prove that size-dependent scalings are unavoidable in Hamiltonian locality reduction. However, if one allows for an additional resource of engineered dissipation, we can circumvent the locality reduction no-go theorem using the quantum Zeno effect. [journal] [arXiv]
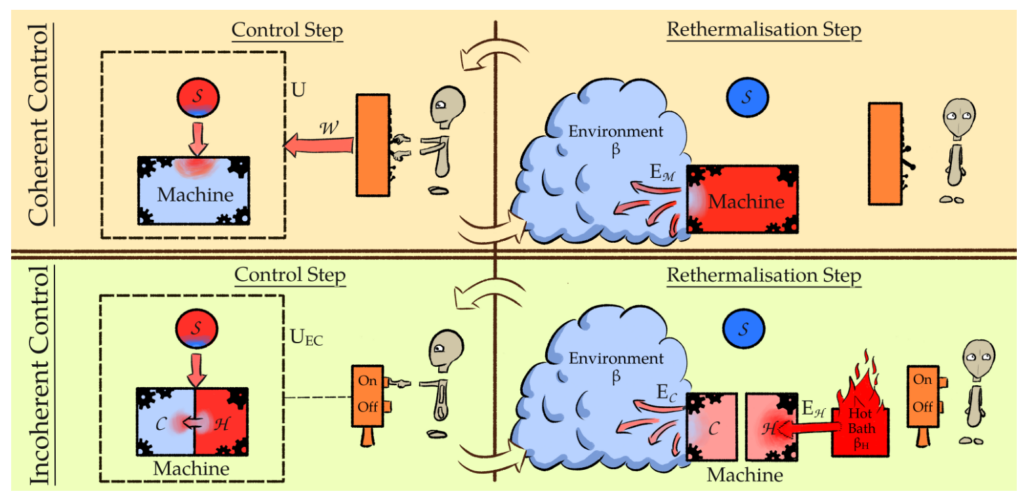
Landauer vs. Nernst: What is the True Cost of Cooling a Quantum System?
with Philip Taranto, Faraj Bakhshinezhad, Ralph Silva, Nicolai Friis, Maximilian P. E. Lock, Giuseppe Vitagliano, Felix C. Binder, Tiago Debarba, Emanuel Schwarzhans, Fabien Clivaz, Marcus Huber
Thermodynamics connects our knowledge of the world to our capability to manipulate and thus to control it. This crucial role of control is exemplified by the third law of thermodynamics, Nernst’s unattainability principle, which states that infinite resources are required to cool a system to absolute zero temperature. But what are these resources and how how does this relate to Landauer’s principle that famously connects information and thermodynamics? We answer these questions by showing that perfect cooling is possible with Landauer energy cost given infinite time or control complexity. However, such optimal protocols require complex unitaries generated by an external work source. Restricting to unitaries that can be run solely via a heat engine, we derive a novel Carnot-Landauer limit, along with protocols for its saturation. This generalizes Landauer’s principle to a fully thermodynamic setting, leading to a unification with the third law and emphasizes the importance of control in quantum thermodynamics. [journal] [arXiv]
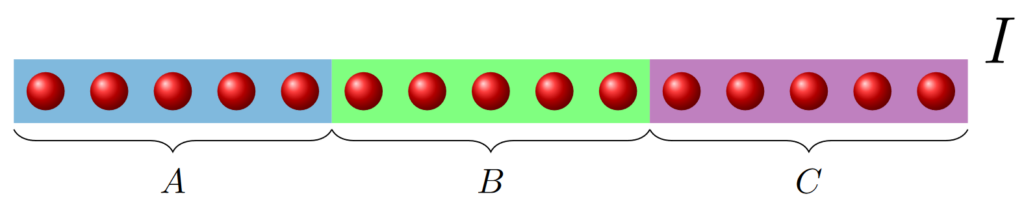
Exponential decay of mutual information for Gibbs states of local Hamiltonians
with Ángela Capel and Antonio Pérez-Hernández
The thermal equilibrium properties of physical systems can be described using Gibbs states. It is therefore of great interest to know when such states allow for an easy description. In particular, this is the case if correlations between distant regions are small. In this work, we consider 1D quantum spin systems with local, finite-range, translation-invariant interactions at any temperature. In this setting, we show that Gibbs states satisfy uniform exponential decay of correlations and, moreover, the mutual information between two regions decays exponentially with their distance, irrespective of the temperature. In order to prove the latter, we show that exponential decay of correlations of the infinite-chain thermal states, exponential uniform clustering and exponential decay of the mutual information are equivalent for 1D quantum spin systems with local, finite-range interactions at any temperature. [journal] [arXiv]
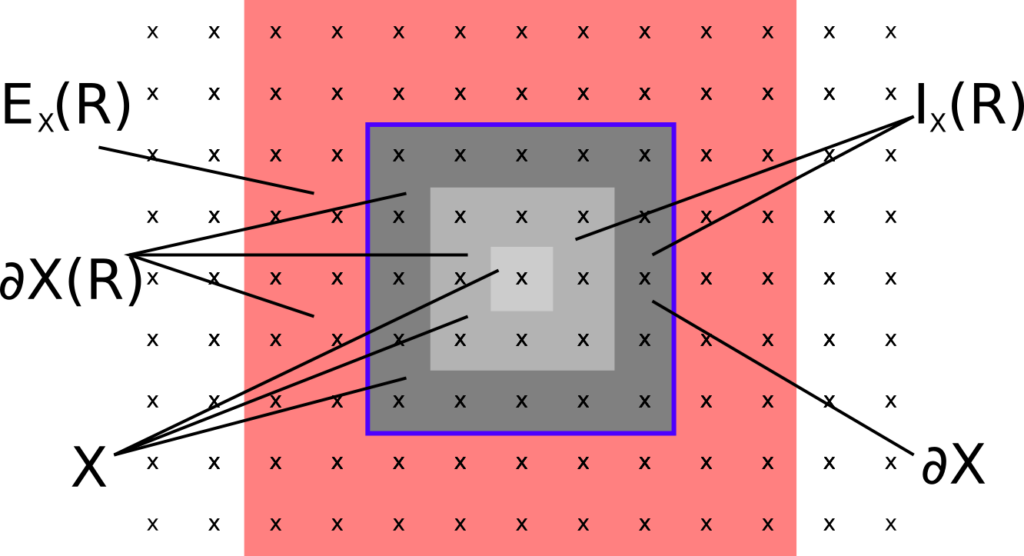
Local factorisation of the dynamics of quantum spin systems
with Sven Bachmann
We are motivated by the study of area laws for the entanglement entropy of gapped ground states of quantum spin systems and their stability. These area laws state that the entanglement entropy of an area X scales with the boundary, not the volume, thereby suggesting that there is no long-range entanglement. We prove that the unitary cocycle generated by a local time-dependent Hamiltonian can be approximated, for any finite set X, by a tensor product of the corresponding unitaries in X and its complement, multiplied by a dynamics strictly supported in the neighbourhood of the surface ∂X. The error decays almost exponentially in the size of the neighbourhood and grows with the square of the area |∂X|2. [journal] [arXiv]