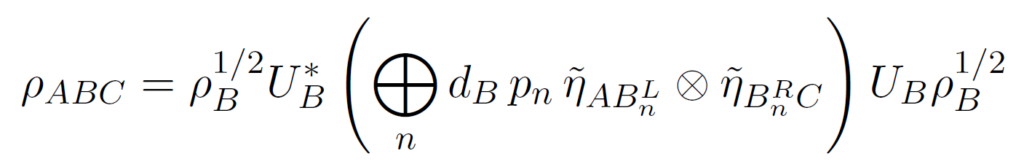
Belavkin-Staszewski Quantum Markov Chains
with Ángela Capel, Pablo Costa Rico, and Anna Jenčová
It is well-known that the conditional mutual information of a quantum state is zero if, and only if, the quantum state is a quantum Markov chain. Replacing the Umegaki relative entropy in the definition of the conditional mutual information by the Belavkin-Staszewski (BS) relative entropy, we obtain the BS-conditional mutual information, and we call the states with zero BS-conditional mutual information Belavkin-Staszewski quantum Markov chains. In this article, we establish a correspondence which relates quantum Markov chains and BS-quantum Markov chains. This correspondence allows us to find a recovery map for the BS-relative entropy in the spirit of the Petz recovery map. Moreover, we prove a structural decomposition of the Belavkin-Staszewski quantum Markov chains and also study states for which the BS-conditional mutual information is only approximately zero. As an application, we show that the conditional mutual information of the state associated to the Gibbs state of a quantum spin chain with local, finite-range, translation-invariant interactions at any positive temperature via this new correspondence decays superexponentially fast with the size of the middle system. [arXiv]

Unified framework for continuity of sandwiched Rényi divergences
with Ángela Capel, Paul Gondolf, and Tim Möbus
Rényi entropies are used to describe how well one can perform tasks in quantum information theory such as hypothesis testing. In this work, we prove uniform continuity bounds for entropic quantities related to the sandwiched Rényi divergences, e.g., the sandwiched Rényi conditional entropy. We follow three different approaches: The first one is the axiomatic approach, which exploits the sub-/ superadditivity and joint concavity/ convexity of the exponential of the divergence. In our second approach, termed the “operator space approach”, we express the entropic measures as norms and utilize their properties for establishing the bounds. These norms draw inspiration from interpolation space norms. Finally, we merge the approaches into a mixed approach that has some advantageous properties and then discuss in which regimes each bound performs best. Our results improve over the previous best continuity bounds or sometimes even give the first continuity bounds available. [journal] [arXiv]
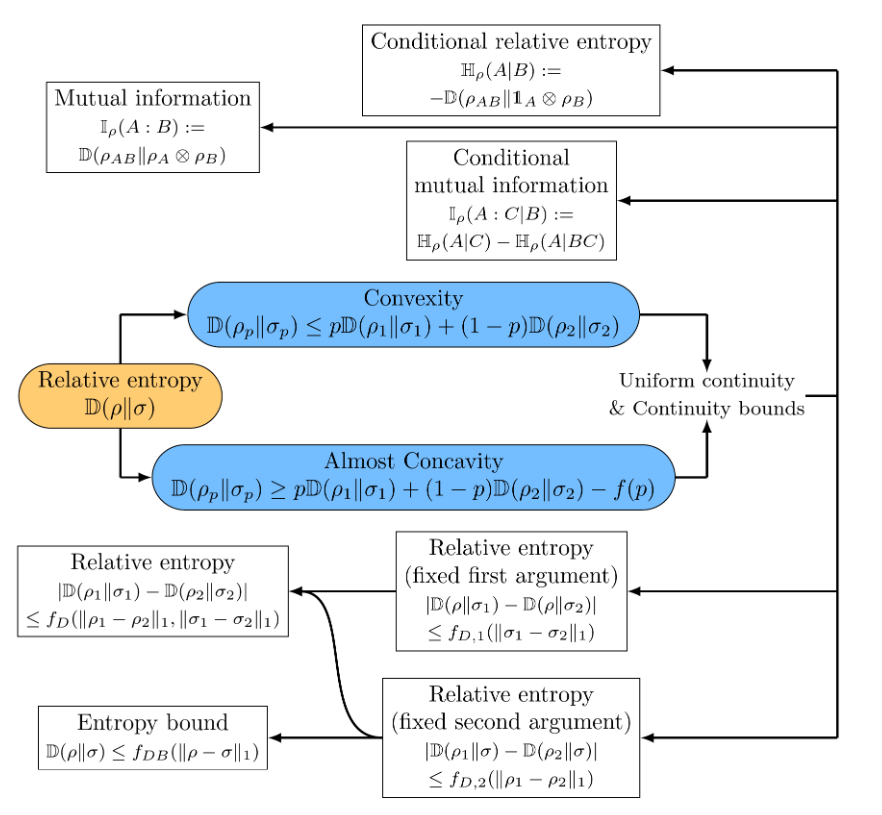
General continuity bounds for quantum relative entropies
with Ángela Capel, Paul Gondolf, and Antonio Pérez-Hernández
Entropies are ubiquitous in (quantum) information theory, because they quantify how well one can do different communication tasks. In this article, we generalize a proof technique by Alicki, Fannes and Winter and introduce a method to prove continuity bounds for entropic quantities derived from different quantum relative entropies. For the Umegaki relative entropy, we mostly recover known almost optimal bounds, whereas, for the Belavkin-Staszewski relative entropy, our bounds are new. Finally, we use these continuity bounds to derive a new entropic uncertainty relation. This paper is a short version of previous paper by the same authors. [proceedings] [arXiv]
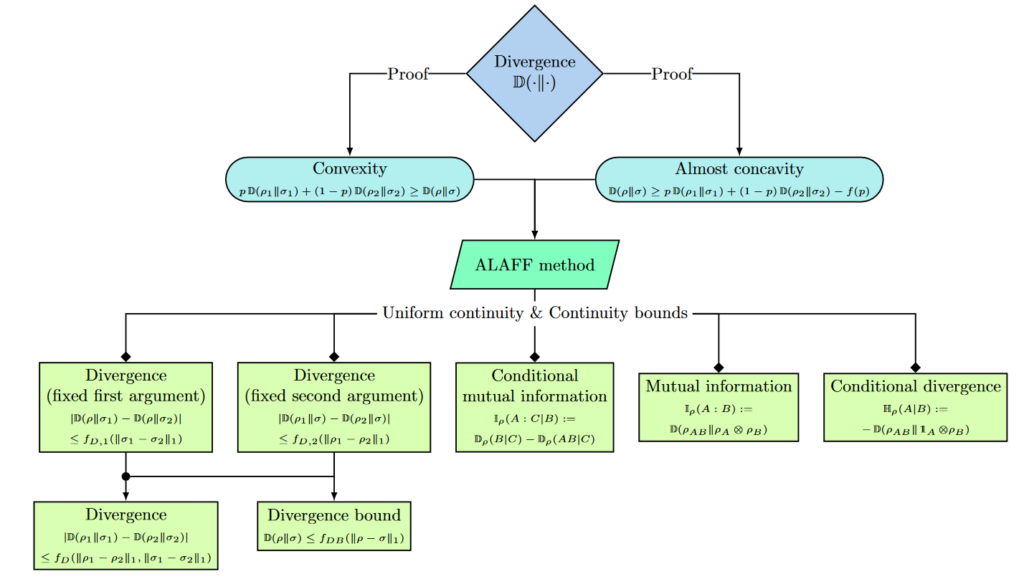
Continuity of quantum entropic quantities via almost convexity
with Ángela Capel, Paul Gondolf, and Antonio Pérez-Hernández
Entropic quantities are the building blocks of quantum information theory. Based on the proofs of the continuity of the conditional entropy by Alicki, Fannes, and Winter, we introduce in this work the almost locally affine (ALAFF) method. This method allows us to prove a great variety of continuity bounds for the derived entropic quantities, all from a single theorem. First, we apply the ALAFF method to the Umegaki relative entropy. This way, we recover known almost tight bounds, but also some new continuity bounds for the relative entropy. Subsequently, we apply our method to the Belavkin-Staszewski relative entropy (BS-entropy). This yields novel explicit bounds in particular for the BS-conditional entropy, the BS-mutual and BS-conditional mutual information. On the way, we also prove almost concavity for the Umegaki relative entropy and the BS-entropy. There is a short version of this paper. [journal] [arXiv]
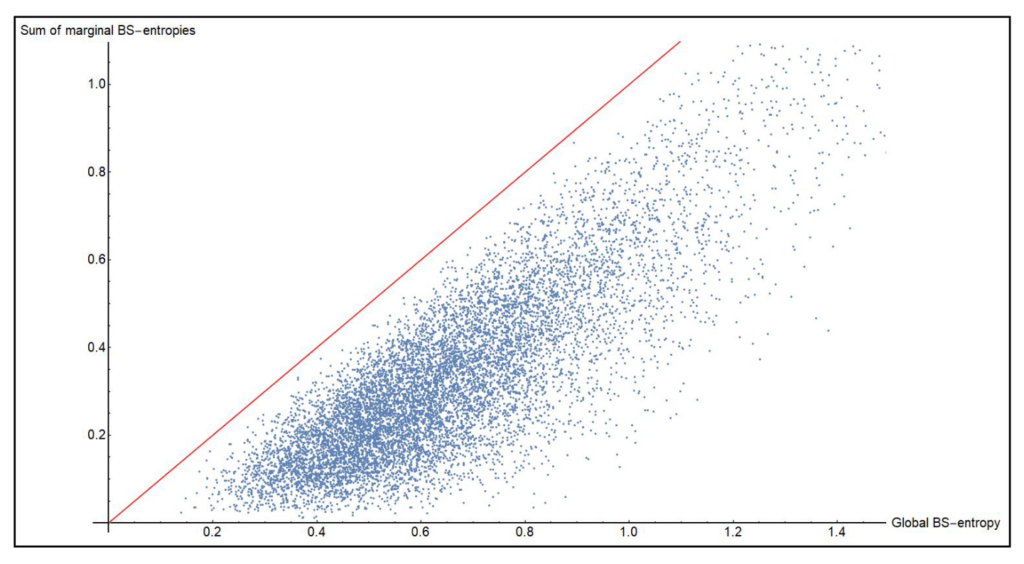
Weak quasi-factorization for the Belavkin-Staszewski relative entropy
with Ángela Capel and Antonio Pérez-Hernández
Quasi-factorization-type inequalities for the relative entropy have recently proven to be fundamental in modern proofs of modified logarithmic Sobolev inequalities for quantum spin systems. In this paper, we show some results of weak quasi-factorization for the Belavkin-Staszewski relative entropy, i.e. upper bounds for the BS-entropy between two bipartite states in terms of the sum of two conditional BS-entropies, up to some multiplicative and additive factors. [proceedings] [arXiv]
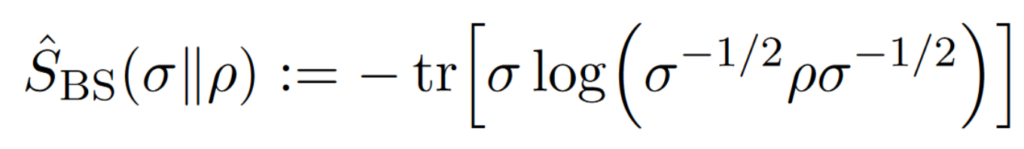
A strengthened data processing inequality for the Belavkin-Staszewski relative entropy
with Ángela Capel
In this work, we provide a strengthening of the data processing inequality for the relative entropy introduced by Belavkin and Staszewski (BS-entropy). This extends previous results by Carlen and Vershynina for the relative entropy and other standard f-divergences. To this end, we provide two new equivalent conditions for the equality case of the data processing inequality for the BS-entropy. Subsequently, we extend our result to a larger class of maximal f-divergences. [journal] [arXiv]