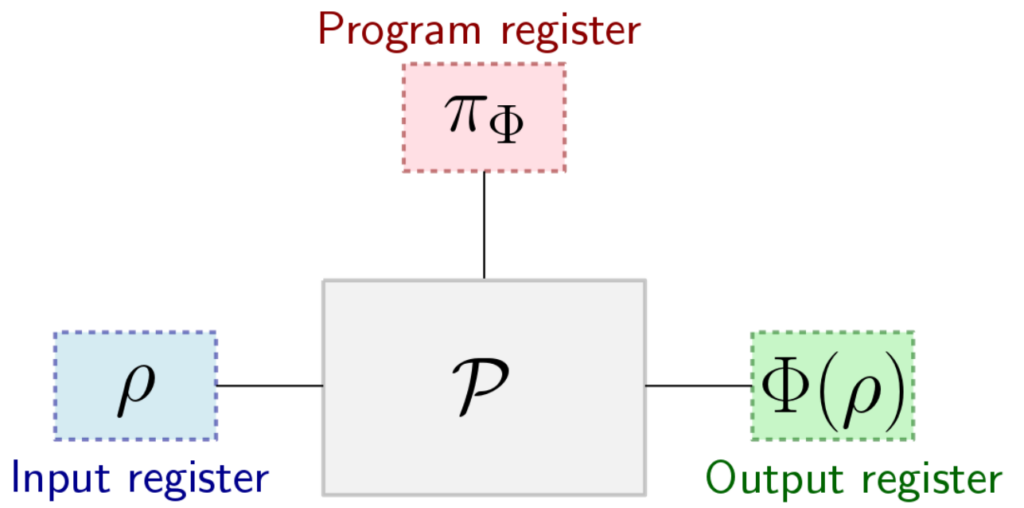
Programmability of covariant quantum channels
with Martina Gschwendtner and Andreas Winter
A programmable quantum processor uses the states of a program register to specify one element of a set of quantum channels which is applied to an input register. It is well-known that such a device is impossible with a finite-dimensional program register for any set that contains infinitely many unitary quantum channels (Nielsen and Chuang’s No-Programming Theorem), meaning that a universal programmable quantum processor does not exist. The situation changes if the system has symmetries. Indeed, here we consider group-covariant channels. We prove that if the group acts irreducibly on the channel input, these channels can be implemented exactly by a programmable quantum processor (via teleportation simulation, which uses the Choi-Jamiolkowski state of the channel as a program). We also prove that this construction is optimal. [journal] [arXiv]
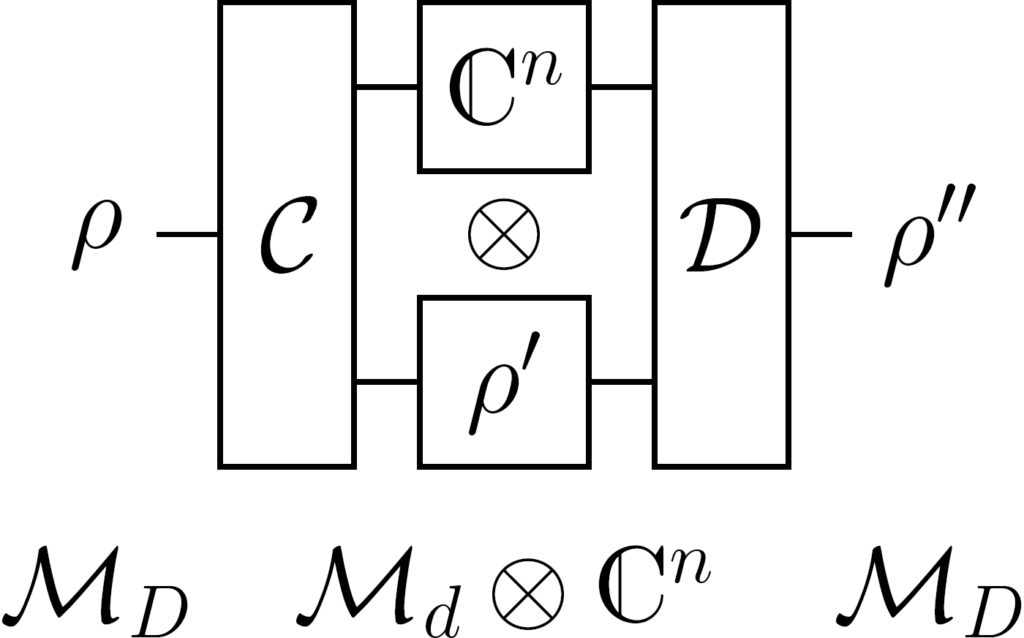
Quantum compression relative to a set of measurements
with Lukas Rauber and Michael M. Wolf
Imagine that you have a quantum state that you would like to measure tomorrow and we already know which observables we are interested in. But until then, we need to store it, using the smallest quantum memory possible. Hence, in this work we investigate the possibility of compressing a quantum system to one of smaller dimension in a way that preserves the measurement statistics of a given set of observables. In this process, we allow for an arbitrary amount of classical side information, since classical storage is much cheaper than quantum storage. Various bounds on the minimal compression dimension are proven and an SDP-based algorithm for its computation is provided. [journal] [arXiv]
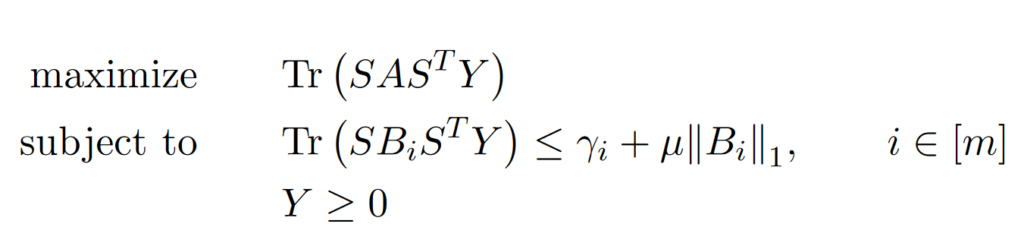
Dimensionality reduction of SDPs through sketching
with Daniel Stilck França
Semidefinite programs (SDPs) are a class of convex optimization problems that appear in all kinds of contexts, for example in quantum information theory, and which we can efficiently solve in practice. We show how to positive maps to SDPs in order to reduce their dimension. More precisely, we use Johnson-Lindenstrauss transforms to produce a smaller SDP whose solution preserves feasibility or approximates the value of the original problem with high probability. These techniques allow to improve both complexity and storage space requirements. Furthermore, we provide some results which clarify the limitations of this approach. [journal] [arXiv]