Inclusion constants for free spectrahedra with applications to quantum incompatibility
with Eric Evert, Igor Klep, Victor Magron, and Ion Nechita
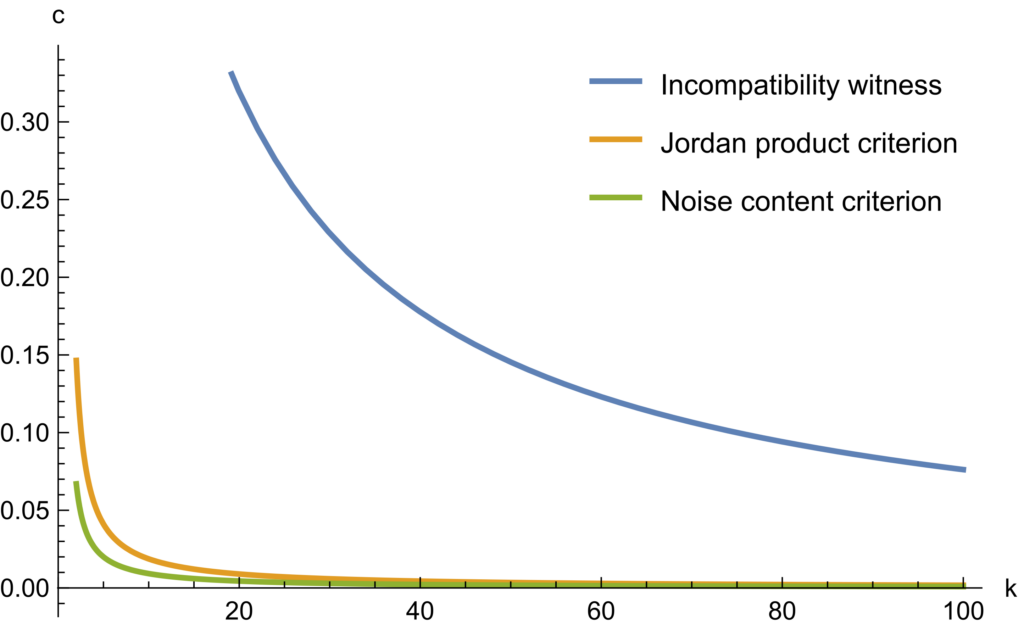
Building on the matrix cube problem, inclusions of free spectrahedra have been used successfully to obtain relaxations of hard spectrahedral inclusion problems. The quality of such a relaxation is quantified by the inclusion constant associated with each free spectrahedron. While optimal values of inclusion constants were known in certain highly symmetric cases, no general method for computing them was available. In this work, we show that inclusion constants for Cartesian products of free simplices can be computed using methods from non-commutative polynomial optimization, together with a detailed analysis of the extreme points of the associated free spectrahedra. This analysis also yields new closed-form analytic expressions for these constants. As an application to quantum information theory, we prove new bounds on the amount of white noise that incompatible measurements can tolerate before they become compatible. In particular, we study the case of one dichotomic and one k-outcome measurement, as well as the case of four dichotomic qubit measurements. [arXiv]
Random measurements are almost maximally incompatible
with Cécilia Lancien and Ion Nechita
In this work, we investigate the incompatibility of random quantum measurements. Most previous work has focused on characterizing the maximal amount of white noise that any fixed number of incompatible measurements with a fixed number of outcomes in a fixed dimension can tolerate before becoming compatible. This can be used to quantify the maximal amount of incompatibility available in such systems. The present article investigates the incompatibility of several classes of random measurements, i.e., the generic amount of incompatibility available. In particular, we show that for an appropriate choice of parameters, both random dichotomic projective measurements and random basis measurements are close to being maximally incompatible. We use the technique of incompatibility witnesses to certify incompatibility and combine it with tools from random matrices and free probability. [arXiv]
Factorization of multimeters: a unified view on nonclassical quantum phenomena
with Tim Achenbach, Leevi Leppäjärvi, Ion Nechita, and Martin Plávala
Quantum theory exhibits various nonclassical features, such as measurement incompatibility, contextuality, steering, and Bell nonlocality, which distinguish it from classical physics. These phenomena are often studied separately, but they possess deep interconnections. This work introduces a unified mathematical framework based on commuting diagrams that unifies them. By representing collections of measurements (multimeters) as maps to the set of column-stochastic matrices, we show that measurement compatibility and simulability correspond to specific factorizations of these maps through intermediate systems. We apply this framework to put forward connections between different nonclassical notions and provide factorization-based characterizations for steering assemblages and Bell correlations, including a new perspective on the CHSH inequality witnessing measurement incompatibility. Inspired by entanglement theory, we also investigate the symmetric n-extensions of multimeters and no-signaling behaviors and connect these extensions to a notion of n-wise compatibility and to the existence of n-wise LHV models, respectively. Furthermore, we investigate robustness to noise of nonlocal features by examining factorization conditions for maps involving noisy state spaces, providing geometric criteria for when noisy multimeters can be simulated by simpler measurement settings. [arXiv]
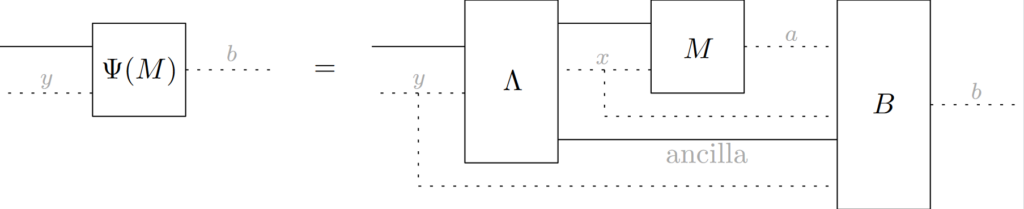
On the simulation of quantum multimeters
with Leevi Leppäjärvi and Ion Nechita
In this work, we study what it means to simulate a collection of measurements, which we call a multimeter. To this end, we first explicitly characterize the completely positive transformations between multimeters. However, not all of these transformations correspond to valid simulations, as exemplified by the existence of maps that always prepare the same multimeter regardless of the input, which we call trash-and-prepare. We give a new definition of multimeter simulations as transformations that are triviality-preserving, i.e., when given a multimeter consisting of trivial measurements they can only produce another trivial multimeter. In the absence of a quantum ancilla, we then characterize the transformations that are triviality-preserving and the transformations that are trash-and-prepare. Finally, we use these characterizations to compare our new definition of multimeter simulation to three existing ones: classical simulations, compression of multimeters, and compatibility-preserving simulations. [journal] [arXiv]
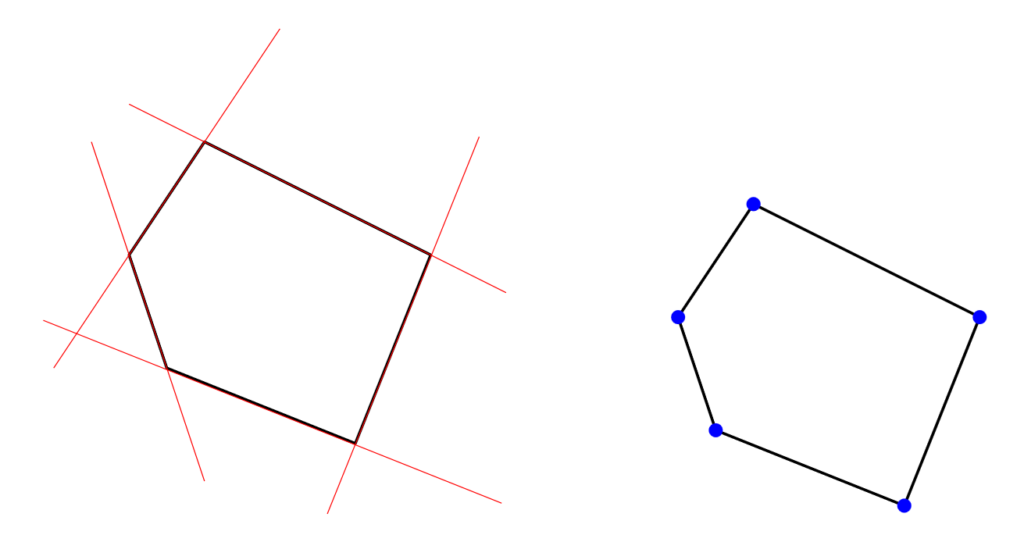
Polytope compatibility – from quantum measurements to magic squares
with Ion Nechita and Simon Schmidt
Several central problems in quantum information theory (such as measurement compatibility and quantum steering) can be rephrased as membership in the minimal matrix convex set corresponding to special polytopes (such as the hypercube or its dual). In this article, we generalize this idea and introduce the notion of polytope compatibility, by considering arbitrary polytopes. We find that semiclassical magic squares correspond to Birkhoff polytope compatibility. In general, we prove that polytope compatibility is in one-to-one correspondence with measurement compatibility, when the measurements have some elements in common and the post-processing of the joint measurement is restricted. [journal] [arXiv]

A tensor norm approach to quantum compatibility
with Ion Nechita
Measurement incompatibility is one of the most striking examples of how quantum physics is different from classical physics. Two measurements are incompatible if they cannot arise via classical post-processing from a third one. A natural way to quantify incompatibility is in terms of noise robustness. In the present article, we review recent results on the maximal noise robustness of incompatible measurements, which have been obtained by the present authors using free spectrahedra, and rederive them using tensor norms. We also describe incompatibility witnesses using tensor norm and matrix convex set duality, emphasizing the relation between the different notions of witnesses. [journal] [arXiv]
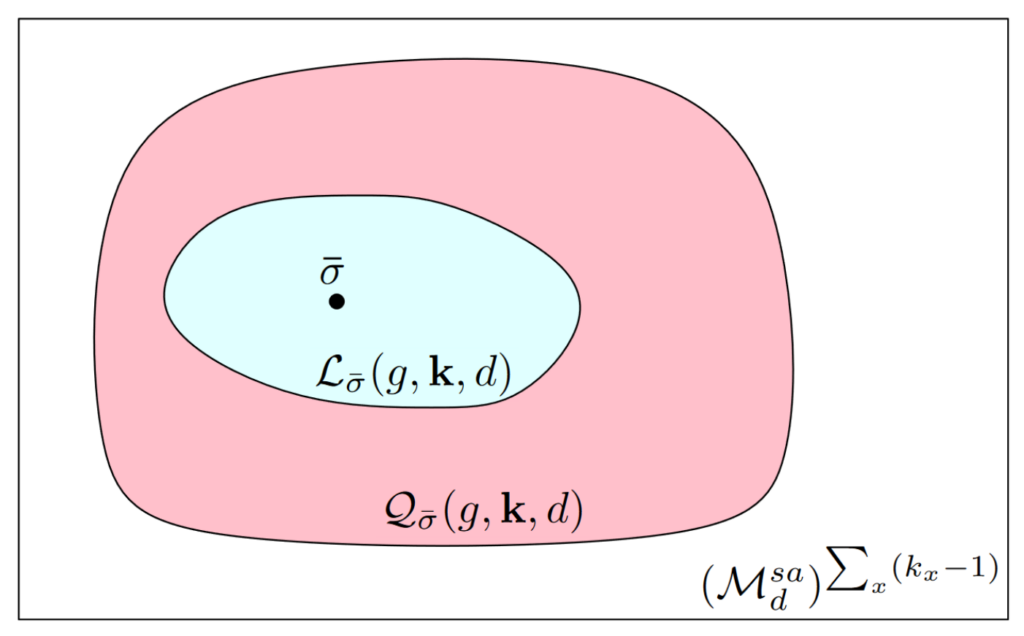
Maximal violation of steering inequalities and the matrix cube
with Ion Nechita
A quantum state is steerable if Alice can prove to a mistrustful Bob that they share an entangled state. In this work, we characterize the amount of steerability present in quantum theory by connecting the maximal violation of a steering inequality to an inclusion problem of free spectrahedra. In particular, we show that the maximal violation of an arbitrary unbiased dichotomic steering inequality is given by the inclusion constants of the matrix cube, which is a well-studied object in convex optimization theory. This allows us to find new upper bounds on the maximal violation of steering inequalities and to show that previously obtained violations are optimal. [journal] [arXiv]
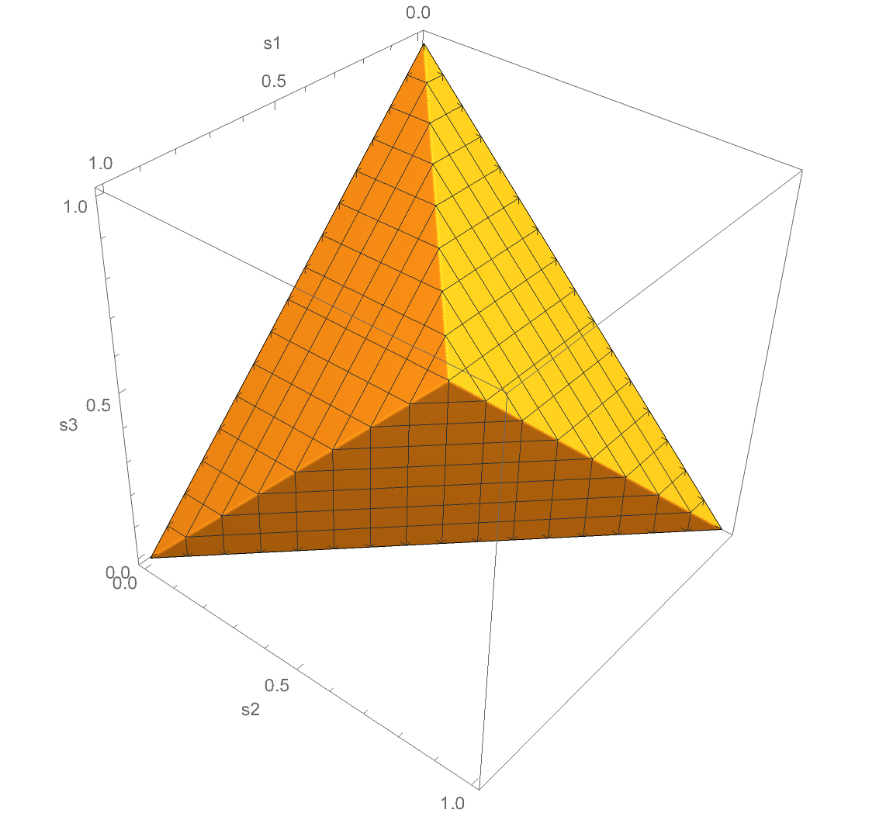
Incompatibility in general probabilistic theories, generalized spectrahedra, and tensor norms
with Anna Jenčová and Ion Nechita
In this work, we investigate measurement incompatibility in general probabilistic theories (GPTs). The latter generalize quantum mechanics and studying them helps us to understand in how far quantum mechanics is special as a theory of nature. We show several equivalent characterizations of compatible measurements. The first is in terms of the positivity of associated maps. The second relates compatibility to the inclusion of certain generalized spectrahedra. The third characterization connects the compatibility of dichotomic measurements to the ratio of tensor crossnorms of Banach spaces. We use these characterizations to study the amount of incompatibility present in different GPTs. For centrally symmetric GPTs, we show that the compatibility degree is given as the ratio of the injective and the projective norm of the tensor product of associated Banach spaces. This allows us to completely characterize the compatibility regions of several GPTs, and to obtain optimal universal bounds on the compatibility degree in terms of the 1-summing constants of the associated Banach spaces. [journal] [arXiv]
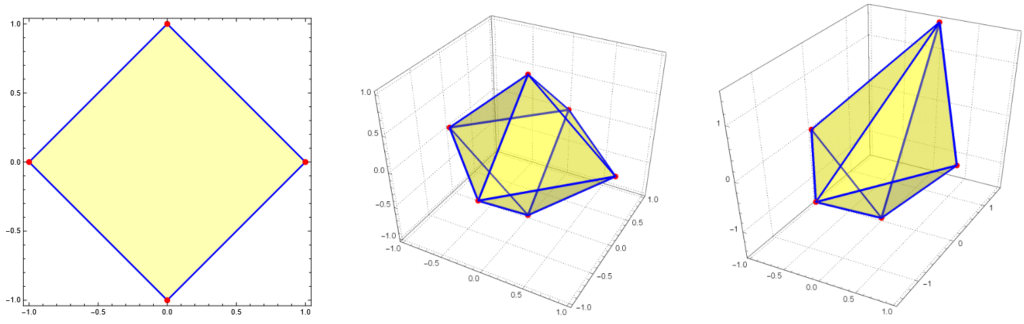
Compatibility of quantum measurements and inclusion constants for the matrix jewel
with Ion Nechita
In this work, we establish the connection between the study of free spectrahedra and the compatibility of quantum measurements with an arbitrary number of outcomes. This generalizes previous results by the authors for measurements with two outcomes. A particular free spectrahedron which we define in this work is the matrix jewel. We find that the compatibility of arbitrary measurements corresponds to the inclusion of the matrix jewel into a free spectrahedron defined by the effect operators of the measurements under study. [journal] [arXiv]
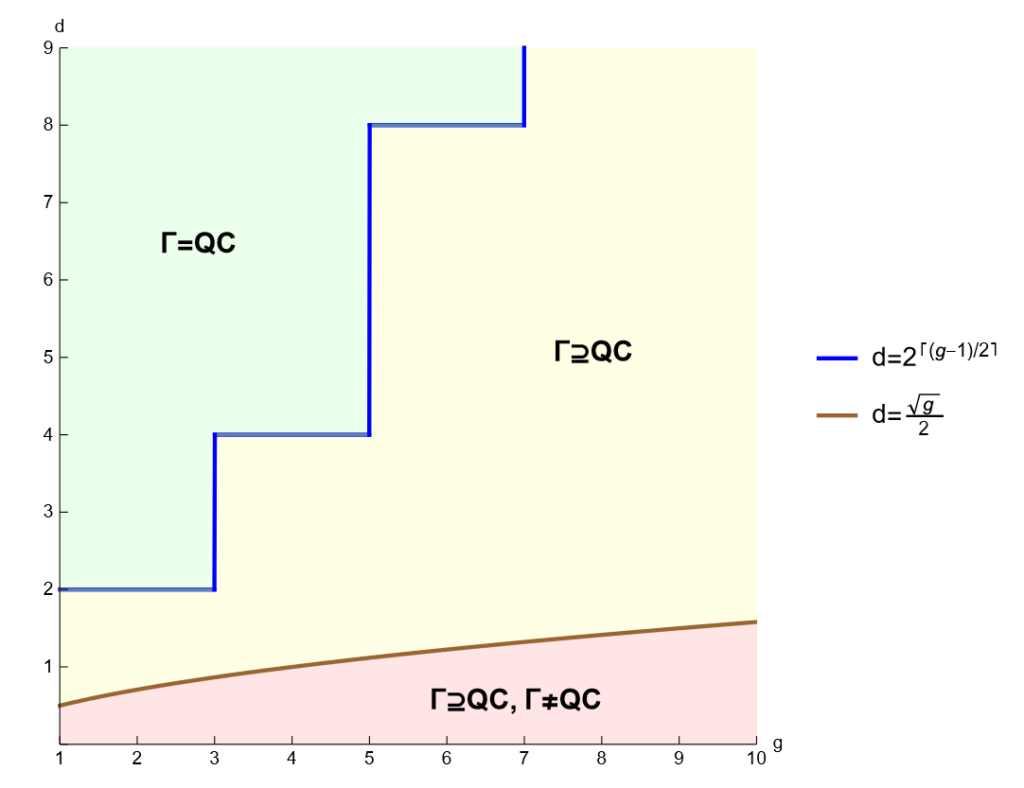
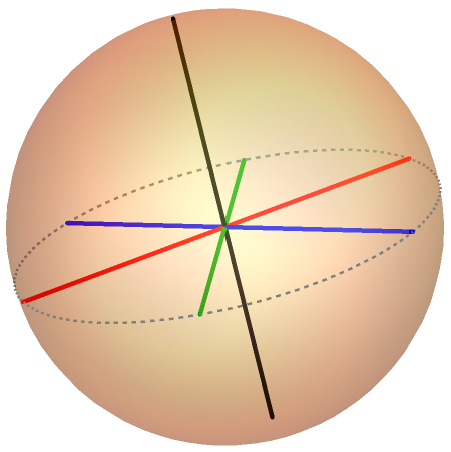
Joint measurability of quantum effects and the matrix diamond
with Ion Nechita
In this work, we investigate the joint measurability of dichotomic quantum measurements and connect it to the study of free spectrahedra. Free spectrahedra typically arise as matricial relaxations of linear matrix inequalities. An example of a free spectrahedron is the matrix diamond, which is a matricial relaxation of the ℓ1-ball. We find that joint measurability of dichotomic POVMs is equivalent to the inclusion of the matrix diamond into the free spectrahedron defined by the effects under study. This connection allows us to use results about inclusion constants from free spectrahedra to quantify the degree of incompatibility of quantum measurements. In particular, we completely characterize the case in which the dimension is exponential in the number of measurements. [journal] [arXiv]